CR10018 Steel Threaded Rod Load Data

The data presented below applies to threaded rods capabilities in various use cases.
For all calculations the assumed tensile strength of CR10018 rod is 63.8 ksi, the yield strength is 53.7 ksi, and the modulus of elasticity is 29000 ksi. The stock diameter of 3/8 rods are taken at 0.342" and the stock diameter of a 5/16 rod is taken at 0.278". Max compression is assumed at the point which the threads would shear assuming there is one times diameter thread engagement of a threaded rod at the minor major diameter and a nut at the max pitch diameter assuming no buckling of the rod occurs.
Looking at the strength data for a rod in tension and compressions, the data is as follows:

For 5/16 rods 3.5 inches or shorter and 3/8 rods 4.5 inches or shorter the number above can be used for the max compression strength. For all rod lengths greater than 3.5 inches or 4.5 inches respectively, the buckling of the rod will be the cause of failure so the chart and equations below can be used to determine the max compression force.
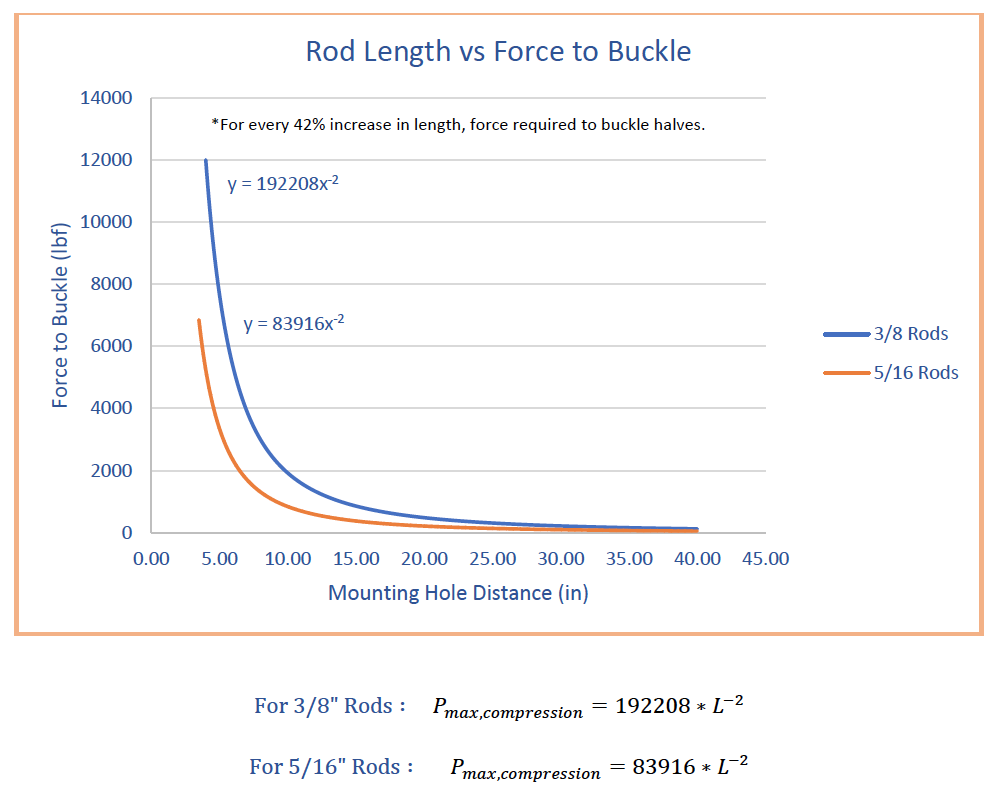
Using the above equations will give a good estimate of the max compression capability of a rod given the length of the rod or assumed mounting hole center to center length. This is the max compression assuming the point of failure occurs due to buckling of the rod. It is possible for short rods with minimal thread engagement to fail at the threads prior to buckling occurring. Max compression in chart is not guaranteed as many factors must be considered to calculate the shear force capability of a thread. The tension values in charts are based solely off the tensile shear stress area of the rod and its Ultimate Tensile Strength. Safety factors as shown in the tables below should be applied to all the numbers above for the best results.
For determining safety factors and dynamic load capacity use the following:

If you have any questions regarding our threaded load data or would like to learn more information, contact us today or call us directly at (920) 235-3710.

